Jordan Ellenberg, nel libro “I numeri non sbagliano mai”, ci guida nel sorprendente mondo della matematica: una lente per capire meglio anche il nostro presente e, solo per fare un esempio, i meccanismi che regolano il social network più famoso – Su ilLibraio.it il capitolo “Facebook sa che siete terroristi?”
Non sempre la matematica è complicata e oscura. Esiste anche una matematica semplice ma profonda che aiuta a orientarsi nella vita, e con I numeri non sbagliano mai (Ponte alle Grazie) Jordan Ellenberg ci guida alla scoperta del suo potere: come una lente magica, il ragionamento matematico penetra la superficie caotica della realtà per rivelarci ciò che l’intuito e il buonsenso non ci permettono di cogliere.
Esiste un sistema di voto equo? Qual è stato il peggior genocidio del XX secolo? Che cosa lega la geometria non euclidea alla pittura rinascimentale? Tra trent’anni saremo tutti obesi? A queste e a tante altre domande risponde Ellenberg, professore di matematica alla University of Wisconsin-Madison, in questo suo primo librp di divulgazione matematica.
Su ilLibraio.it un estratto dedicato a un tema attuale e provocatorio:
Facebook sa che siete terroristi?
Dunque, se le multinazionali che hanno accesso a enormi quantità di dati, hanno ancora notevoli limiti riguardo a ciò che riescono a «sapere» di voi, di che cosa dovreste preoccuparvi?
Provate a preoccuparvi di questo. Immaginate che Facebook decida di sviluppare un metodo per tentare di individuare quali dei suoi utilizzatori potrebbero essere coinvolti in attività terroristiche contro gli Stati Uniti. Dal punto di vista matematico il problema non è diverso da quello di stabilire se un cliente di Netflix potrà apprezzare Ocean’s 13. In genere Facebook conosce i veri nomi e gli indirizzi dei suoi utilizzatori, perciò può usare i documenti pubblici per generare un elenco di profili Facebook di persone che sono già state condannate per reati terroristici o per aver fiancheggiato gruppi terroristici. Dopodiché interviene la matematica. I terroristi tendono ad aggiornare il loro stato quotidiano più spesso rispetto alla popolazione generale degli utilizzatori di Facebook, oppure meno spesso, oppure, sulla base di questa metrica, risultano sostanzialmente indistinguibili dalla massa? Ci sono specifiche parole che compaiono più di frequente nei loro aggiornamenti? Gruppi musicali o squadre sportive o prodotti verso cui tendono a manifestare un gradimento o un’avversione insoliti?
Mettendo insieme tutti questi elementi, possiamo assegnare a ogni utilizzatore di Facebook un punteggio che rappresenta la nostra miglior stima possibile della probabilità che quell’utilizzatore abbia legami, o avrà legami futuri con gruppi terroristici. È più o meno la stessa cosa che fa Target quando incrocia i dati relativi ai vostri acquisti di lozioni e integratori di vitamine per valutare la probabilità che siate incinte. C’è però un’importante differenza: le gravidanze sono molto comuni mentre i terroristi sono molto rari. Nella quasi totalità dei casi, la probabilità stimata che un dato utilizzatore di Facebook sia un terrorista risulterebbe molto piccola. Perciò il progetto non avrebbe nulla da spartire con l’agenzia Precrimine di Minority Report: l’algoritmo panottico di Facebook non sarebbe in grado di sapere che state per compiere un delitto prima che lo compiate. Pensate invece a qualcosa di molto più modesto; per esempio a un elenco di centomila utilizzatori riguardo ai quali Facebook può affermare con un certo grado di sicurezza che «le persone in quest’elenco hanno una probabilità doppia rispetto all’utilizzatore tipico di Facebook di essere terroristi o simpatizzanti del terrorismo». Che cosa fareste se scopriste che un tizio che vive nel vostro isolato fa parte dell’elenco? Chiamereste l’FBI?
Prima di compiere il passo, disegniamo un altro riquadro.
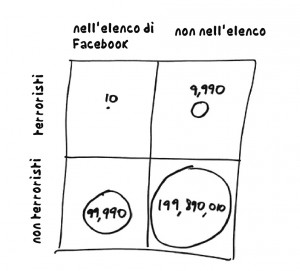
All’interno del riquadro ci sono i circa 200 milioni di cittadini statunitensi che utilizzano Facebook. La linea che divide la metà inferiore da quella superiore separa i futuri terroristi (in alto) dagli innocenti (in basso). Qualsiasi cellula terroristica presente negli Stati Uniti è sicuramente molto piccola; diciamo, per essere il più paranoidi possibile, che ci sono diecimila persone che i federali farebbero meglio a tenere d’occhio. Significa un individuo ogni ventimila nel totale della base di utilizzatori.
La linea di separazione tra destra e sinistra è quella tracciata da Facebook: sul lato sinistro ci sono i centomila individui che secondo Facebook hanno una probabilità elevata di essere coinvolti nel terrorismo. Prenderemo Facebook alla lettera e immagineremo che il suo algoritmo sia così efficace da individuare tutti coloro che hanno una probabilità doppia di essere terroristi rispetto all’utilizzatore medio. Perciò in questo gruppo, dieci persone in tutto, cioè una ogni diecimila, saranno effettivamente terroristi, mentre 99.990 non lo saranno. Se dieci di 10.000 futuri terroristi si trovano nel settore in alto a sinistra del riquadro, allora ne restano 9990 in quello in alto a destra. Applicando lo stesso ragionamento, scopriamo che ci sono 199.990.000 non terroristi nella base di utilizzatori di Facebook, 99.990 dei quali sono stati segnalati dall’algoritmo e occupano il settore in basso a sinistra, il che ne lascia 199.890.010 in quello in basso a destra. Se sommiamo i quattro settori, otteniamo 200.000.000, cioè il totale degli utilizzatori di Facebook.
Il vicino che abita nel vostro stesso isolato si trova da qualche parte in questo riquadro diviso in quattro parti. Ma dove? Sappiamo solo che deve trovarsi nella metà sinistra, dato che Facebook l’ha identificato come potenziale terrorista. La cosa interessante da notare è che quasi nessuno di coloro che si trovano nella metà sinistra del riquadro è un terrorista. In effetti, c’è il 99,99 per cento di probabilità che il vostro vicino sia innocente.
Da un certo punto di vista, questa è una rivisitazione del panico scatenato dalle pillole anticoncezionali in Inghilterra. Essere nell’elenco di Facebook raddoppia le probabilità di essere un terrorista, il che sembra terribile. Ma le probabilità di partenza sono molto piccole e perciò quando le si raddoppia continuano a rimanere piccole.
Ma c’è un’altra ottica da cui considerare la questione, un’ottica che evidenzia in modo ancora più chiaro quanto possa essere disorientante e infido ragionare sull’incertezza. Ponetevi questa domanda: se una persona non è un futuro terrorista, quante probabilità ci sono che finisca, ingiustamente, nell’elenco di Facebook? Riferendoci al riquadro, questo significa: se vi trovate nella metà inferiore, quante probabilità ci sono che siate dal lato sinistro? Calcolarlo è abbastanza facile: ci sono 199.990.000 persone nella metà inferiore del riquadro, e di queste solo 99.990 si trovano sul lato sinistro. Perciò la probabilità che un innocente sia etichettato come potenziale terrorista dall’algoritmo di Facebook è
99.990/199.990.000
che equivale a circa lo 0,05 per cento.
Proprio così: una persona innocente ha solo una probabilità su 2000 di essere erroneamente identificata come terrorista da Facebook!
Adesso che cosa pensate del vostro vicino?
Il ragionamento che si usa per determinare i valori p ci offre una guida chiara. Secondo l’ipotesi nulla il nostro vicino non è un terrorista. Se vale quest’ipotesi – cioè se presumiamo che egli sia innocente – la probabilità di trovarlo nella lista nera di Facebook è di appena lo 0,05 per cento, ben al di sotto della soglia di significatività statistica. In altre parole, in base alle regole che governano la gran parte della scienza contemporanea, sareste legittimati a rigettare l’ipotesi nulla e a dichiarare che il vostro vicino è un terrorista. Solo che c’è un 99,99 per cento di probabilità che non lo sia. Da un lato, ci sono pochissime probabilità che un innocente sia segnalato dall’algoritmo. Allo stesso tempo, le persone che l’algoritmo segnala sono quasi tutte innocenti. Sembra un paradosso, ma non lo è. E se prendete un bel respiro e tenete gli occhi sul riquadro, non potete sbagliarvi. Questo è il punto cruciale: in realtà sono due le domande che possiamo porci. Possono sembrare più o meno equivalenti, ma non lo sono.
Domanda n. 1: Qual è la probabilità che una persona finisca nell’elenco di Facebook nel caso in cui non sia un terrorista?
Domanda n. 2: Qual è la probabilità che una persona non sia un terrorista nel caso in cui sia finita nell’elenco di Facebook?
Un modo per capire che queste due domande sono diverse è notare che hanno risposte diverse. Risposte molto diverse. Abbiamo già visto che la risposta alla prima domanda è circa una su 2000, mentre la risposta alla seconda è 99.99 per cento. Ed è la risposta alla seconda domanda quella che vogliamo. Le quantità che si utilizzano in queste domande sono chiamate probabilità condizionate; «la probabilità che si verifichi X nel caso in cui valga Y». E il problema con cui ci stiamo confrontando qui è che la probabilità di X, dato Y, non è uguale alla probabilità di Y, dato X. Se vi sembra che tutto ciò abbia un che di familiare, è perché è così; si tratta esattamente dello stesso problema che abbiamo incontrato con la reductio ad improbabilem. Il valore p è la risposta alla domanda:
«Qual è la probabilità che il risultato sperimentale osservato si verifichi, nel caso in cui l’ipotesi nulla sia corretta?».
Ma ciò che vogliamo determinare è l’altra probabilità condizionale:
«Qual è la probabilità che l’ipotesi nulla sia corretta, nel caso in cui si sia osservato un certo risultato sperimentale?».
Il pericolo nasce proprio dal fatto di confondere la seconda quantità con la prima. E questa confusione si trova ovunque, non solo negli studi scientifici. Quando il pubblico ministero si appoggia al banco della giuria e proclama: «C’è solo una probabilità su cinque milioni, ripeto, UNA probabilità su CINQUE MI-LI-O-NI che il DNA di un UOMO INNOCENTE sia compatibile con quello rinvenuto sulla scena del crimine», sta rispondendo alla domanda n. 1: Quante probabilità ci sono che una persona innocente appaia colpevole? Ma il compito della giuria è rispondere alla domanda n. 2: Quante probabilità ci sono che una persona in apparenza colpevole sia innocente? È una domanda a cui il pm non può aiutare i giurati a rispondere.
L’esempio di Facebook e dei terroristi rende chiaro perché dovremmo preoccuparci degli algoritmi scadenti tanto quanto di quelli buoni, se non di più. Fa accapponare la pelle ed è deplorevole il fatto che siate incinte e Target lo sappia, ma fa accapponare ancora di più la pelle ed è peggio se voi non siete terroristi e Facebook ritiene che lo siate. Probabilmente penserete che Facebook non si sognerebbe mai di compilare un elenco di potenziali terroristi (o evasori fiscali, o pedofili) oppure, nel caso in cui lo compili, di renderlo pubblico. Perché dovrebbe? Che vantaggio economico ne trarrebbe? Forse è così. Ma anche la NSA raccoglie dati sulle persone in America, che siano su Facebook oppure no. A meno che non pensiate che quest’agenzia registri metadati da tutte le vostre telefonate per poter fornire alle compagnie telefoniche consigli sui luoghi in cui installare nuovi ripetitori, significa che sta realizzando qualcosa di simile a una lista nera. I Big Data non hanno poteri magici, non dicono ai federali chi è un terrorista e chi non lo è. Ma non è necessario che abbiano poteri magici per generare elenchi di individui che sono in qualche modo sospetti, ad alto rischio, «persone di interesse». La stragrande maggioranza degli individui in quegli elenchi non avrà nulla a che fare con il terrorismo.
Quanto siete sicuri di non essere uno di loro?